

 |
 |
|
Факторинг Анализ финансовых западных рынков Random 2 3 4 Thousands of Observations 0.04 0.03 0.02 0.01 0.00 -0.01 -0.02 -0.03 -0.04 -0.05 -0.06 РИСУНОК 14.1b Конвергенция последовательного среднего, индекс Доу-Джонса для акций промышленных компаний, пятидневные прибыли: 1888 -1990 гг. 2 ~ --------------- I Random § с 2 со  23456789 Thousands of Observations РИСУНОК 142а Конвергенция последовательного стачдаргаого отклонения, функция Коши. На рисунке 14.2(b) мы видим совсем другую ситуацию. Последовательное стандартное отклонение для данных индекса Доу-Джонса не сходится. Оно заканчивается в 1, потому что временной ряд был нормализован к стандартному отклонению 1, но не сходится. С другой стороны, кажется, что гауссов случайный временной ряд сходится при приблизительно 1(Ю наблюдениях, а большие изменения в стандартном отклонении индекса Доу-Джонса представляют собой скачки -изменения прерывисты. Даже в конце фафика, где мы имеем более 52(Ю наблюдений, появляются разрывы. Кажется, что флуктуации становятся менее сильными, но это происходит вследствие того, что ежедневное изменение в цене меньше влияет на среднее. Рисунок 14.3 - увеличенный снимок конца рисунка 14.2(b). Мы можем видеть, что разрывы продолжаются. Это представляет собой влияние бесконечной дисперсии . Дисперсии совокупности не существует, и использование выборочных дисперсий в качестве оценок может вводить в заблуждение. Существует поразительное сходство между поведением последовательного стандартного отклонения Коши и индексом Доу-Джонса. § га -о  Random - 1.2 0.95 2 3 4 Thousands of Observations РИСУНОК 14.2b Последовательное стандартное отклонение, индекс Доу-Джонса для акций промышленных компаний, пятидневные прибыли: 1888-1990 гг. 1006 1005 1004 .2 1002 > -В 1001 -а 3 с о g 1000 d 999 998 997 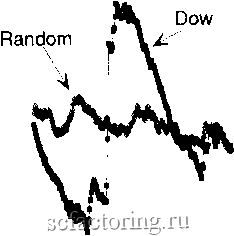 996 - - . . . 4900 4950 5000 5050 5100 5150 5200 5250 5300 5т Number of Observations РИСУНОК 143 Конвергенция последовательного стандартного отклонения, индекс Доу-Джонса для акций промышленных компаний, пятидневные прибыли. Эти фафики подтверждают идею о том, что в долгосрочной перспективе индекс Доу-Джонса характеризуется устойчивым средним и бесконечной памятью, наподобие устойчивых распределений Леви или фрактальных распределений. В этом месте мне необходимо привести некоторые оговорки. Когда я заявляю, что рынок характеризуется бесконечной дисперсией, я не имею в виду, что дисперсия действительно бесконечна. Как и во всех фрактальных структурах, здесь, в конечном счете, есть интервал времени, в котором фрактальное масштабирование перестает работать. В предыдущих главах я говорил, что деревья представляют собой фрактальные структуры. Мы знаем, что ветви дерева не становятся бесконечно малыми. Аналогично, для рыночных прибылей мог бы существовать объем выборки, где дисперсия, действительно, становится конечной. Однако здесь мы можем увидеть, что после более чем 100 лет ежедневных данных стандартное отклонение все еще не сошлось. Следовательно, для всех практических целей рыночные прибыли будут вести себя, как будто они являются бесконечными распределениями дисперсии. По крайней мере, мы можем предположить, что в пределах нашей жизни они будут вести себя, как будто они имеют бесконечную дисперсию. Частные случаи: нормальное распределение и распределение Коши В рамках характеристической функции устойчивых распределений есть два частных случая, которые являются известными распределениями. Используя систему обозначений S(x; а, Р, с, 8) для представления параметров устойчивого распределения X, мы кратко исследуем эти распределения: 1. Для S(x; Z О, с, 5) уравнение (14.3) сводится к: 0(O = i*5*t-(o/2)*t (14.4) где = дисперсия нормального распределения Это стандартный гауссов случай, где с = 2*сг, Если мы также имеем 5 = О, он становится стандартным нормальным распределением со средним О и стандартным отклонением 1. 2. Для S (х; 1,0, с, 5) уравнение (14.4) сводится к: 0(t) = i*8*t-c*t (14.5) Это логарифм характеристической функции для распределения Коши, которое, как известно, имеет бесконечную дисперсию и среднее. В этом случае 5 становится медианой распределения, а с - семи-интерквартильным размахом. Эти два известных распределения, распределение Коши и нормальное распределение, имеют много применений. Они также являются единственными двумя членами семейства устойчивых распределений, для которых могут быть явно вьшедены функции плотности вероятностей. Во всех других дробных случаях они должны быть оценены, обычно посредством численных средств. Мы обсудим один из этих методов в одном из последующих разделов этой главы.
|