

 |
 |
|
Факторинг Анализ финансовых западных рынков 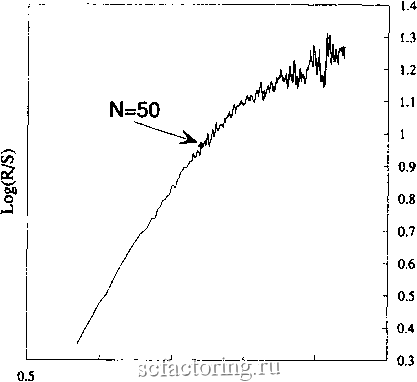 1 1.5 2 2.5 LogCNumber of Observations) РИСУНОК 16.4 R/S-анализ, уравнение Макки-Гласса с системным шумом. Циклы Мы уже обсуждали в Главе б, как R/S-анализ может различить цикл даже в присутствии одного стандартного отклонения наблюдаемого шума. На Рисунке 16.4 показан R/S-анализ уравнения Макки-Гласса с одним включенным стандаргным отклонением системного шума. Показатель Херста фактически идентичен (Н = 0,72), и все еще различимы 50 циклов наблюдений. V-статистика показана на Рисунке 16.5, где цикл снова является легко различимым. Что означает тот факт, что наклон фафика в логарифмическом масштабе по обеим осям переходит к случайному блужданию? Есть два возможных объяснения: 1. Процесс может быть дробным броуновским движением с длинной, но конечной памятью. Причинного объяснения конечной памяти не существует, но она может являться функцией ряда наблюдений. Масштабирование часто останавливается, поскольку для больших значений п не существует достаточного количества наблюдений. 2. Система является шумной хаотической системой и длина конечной памяти измеряет сворачивание апрактора. Расхождение близлежащих орбит в фазовом пространстве означает, что они становятся некоррелироваными после периода обращения (Волф, Свифт, Свини и Вастано (Wolf, Swift, Sweeney, & Vastano, 1985). Поэтому процесс памяти прекращается после орбитального цикла. По существу, длина конечной памяти становится отрезком времени, который требуется системе, чтобы забыть ее начальные условия. С графической точки зрения, когда система проходит через орбиту, она движется по длине аттрактора. Как только она проходит длину аттрактора, диапазон не может больше расти, поскольку аттрактор представляет собой офаниченное множество. Процесс дробного шума не является офаниченным множеством, так что диапазон не прекратит расти. Эта физическая характеристца аттракторов также подходит к характеристикам нормированного размаха. Оба о&ьяснения вероятны, особенно когда мы используем короткие наборы данных. Как нам решить, что есть что? N=50 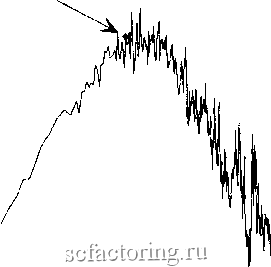 1 1.5 2 2.5 Log(Number of Observations) - 1.4 1.3 1.2 I.l 1 0.9 0.8 0.7 0.6 РИСУНОК 163 V-статистика, уравнение Макки-Гласса с системным шумом. РАЗЛИЧЕНИЕ ШУМОВОГО ХАОСА И ДРОБНОГО ШУМА Самый прямой подход состоит в том, чтобы сымитировать анализ индекса Доу-Джонса для акций промышленных компаний, проведенный в Главе 8. Если разрыв в графике в логарифмическом масштабе по обеим осям действительно представляет собой цикл, а не статистический артефакт, он должен быть независим от приращения времени, используемого в R/S-анализе. Для данных индекса Доу-Джонса цикл всегда составлял 1 040 операционных дней. Когда мы двигались от пятидневных к 20-дневным приращениям, цикл двигался от 208 пятидневных периодов к 52 20-дневным периодам. Если цикл не зависит от объема выборки, мы можем быть достаточно уверены, что мы исследуем шумовой хаос, а не дробный шум. Что касается данных индекса Доу-Джонса, уменьшение размера набора данных на 75 процентов (настолько, насколько задействовано число наблюдений) не затрагивало длину памяти. Это является убедительным доказательством того, что мы измеряем свертку в фазовом пространстве, а не статистический артефакт. Если в начале мы сталкиваемся с маленьким набором данных, это представляет для нас проблему. Мы можем использовать оценку длины цикла как один из компонентов подтверждающего доказательства, но сама по себе она не является решающей. Например, предположим, что мы используем R/S-анализ на наборе данных из 500 наблюдений. Мы находим значимый показатель Херста (0,50 < Н < 1,0) и длину цикла в 50 наблюдений. Это подразумевает, что мы имеем десять циклов наблюдений, при этом каждый цикл состоит из 50 наблюдений. Согласно Волфу и др. (Wolf et al., 1985), такое количество данных является адекватным для оценки наибольшего показателя Ляпунова. Используя метод, описанный Волфом и др., а также Петерсом (Peters, 1991а), мы вычисляем оценку наибольшего показателя Ляпунова. Если этот показатель положителен, у нас есть хорошее основание, чтобы сделать вывод о том, что процесс является хаотическим. Если инверсия наибольшего показателя Ляпунова приблизительно равна длине цикла (как предположил Чен (Chen, 1987)), мы можем быть еще более уверены. Те из вас, кто знаком с моими более ранними исследованиями индекса S&P 500 (Peters, 1991а, 1991b), вспомнят, что это бьшо моим критерием для того, чтобы прийти к выводу, что индекс S&P 5(Ю, в долгосрочной перспективе, хаотичен, как предполагалось в гипотезе фракгального рынка. Результаты спорны, но я полагаю, что выводы, сделанные на основе независимых испытаний, обоснованны. BDS-xecT Три экономиста, Брок, Дечерт и Шейнкман (Brock, Dechert, and Scheinkman, 1987), разработали дополнительное испытание - BDS-тест - которое широко используется учеными. BDS-статистика, вариант корреляционной размерности, в основном измеряет статистическую значимость вычислений корреляционной размерности. Это действенное испытание, позюляющее отличить случайные системы от детерминированного хаоса или от нелинейных стохастических систем. Однако оно не может различить нелинейную детерминированную систему и нелинейную стохастическую систему. По существу, оно находит нелинейную зависимость. При совместном использовании с другими испытаниями на хаос, а также с R/S-анализом, оно может быть очень полезным. Согласно BDS-тесту корреляционные интегралы должны быть нормально распределенными, если изучаемая система независима, очень подобно распределению Н, которое мы обсуждали в Главе 5. Корреляционный интеграл - вероятность того, что любые две точки находятся на определенном расстоянии е друг от друга в фазоюм пространстве. По мере того как мы увеличиваем е, вероятность изменяется согласно фрактальной размерности фазоюго пространства. Корреляционные интегралы рассчитываются согласно следующему уравнению:
|