симации

yi/fl + У2/2 Pn/fn = fu

yjfil + yn/fil +...+ Уп/il =/2/2!,

yiM -f- 2/2M =/iA!, г = 0,2п-1.

(3.3.5)

Здесь fi - г-й момент исходного распределения. Введем обозначения Х{ =2 fi~ fi = fi/i\. Тогда система (3.3.5) переходит в

YVjJjfi. г = 0,2п-1. (3.3.6)

Эта система решается методом, описанным в книге Р.В. Хемминга [90, с. 139-141].

Численные эксперименты показали, что особыми случаями для Нп -аппроксимации являются любые распределения Эрланга порядка к <п . Это вполне естественно, поскольку последние предполагают последовательную систему фаз, тогда как гиперэкспонента - параллельную.

При Я2-аппроксимации задача подбора ее параметров может быть сведена к решению квадратного уравнения. Детальный анализ показывает, что при Я2-аппроксимации обсуждаемых ниже гамма-распределений с параметром О < а < 1 все параметры вещественны и положительны. В случае 1 < а < 2 одна из вероятностей {t/j} будет отрицательной, а другая превысит единицу. Как показали вычислительные эксперименты, столь парадоксальные промежуточные результаты не мешают успешному расчету систем обслуживания. Наконец, при а > 2 параметры Я2-аппроксимации будут комплексными сопряженными. Эта возможность порождает комплексные вероятности состояний рассчитываемых систем и соответственно удваивает расход памяти при машинном счете.

3.3.2. Гамма-распределение

Гамма-распределение имеет плотность

где Г(а) - гамма-функция со свойствами

Г(а) Г(1)

Г(а + 1) = аГ(а).

= j

= 1,

(3.3.8)

Оно является обобщением распределения Эрланга на случай нецелых а > О . Поэтому его нельзя считать фазовым. На рис. 3.3 показано несколько типичных графиков гамма-плотности с одинаковым средним a i = 1 и различными а . Случай а - I соответствует показательному закону.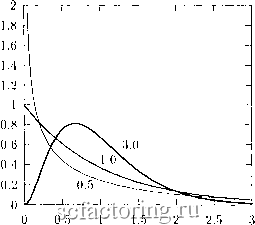

Рис. 3.3. Гамма-плотности

Моменты Г-распределения вычисляются по формулам типа (3.3.3) с заменой г на а . Его дисперсия D ~ f2 - fl - а/р? , а коэффициент вариации v = 1/л/а .

Снятие требования целочисленности а позволяет обеспечить точное выравнивание двух моментов, если положить

(3.3.9)

Для выравнивания большего числа моментов приходится применять гамма-плотность с поправочным многочленом. Удобно подобрать а \л ц

согласно (3.3.9), после чего нетрудно сформировать систему линейных уравнений относительно коэффициентов поправочного многочлена Ч

3.3.3. Нормальное распределение

На рис. 3.4 приведены графики играющего важнейшую роль в теории вероятностей и математической статистике нормального распределения с плотностью /(.г) = ехр[-(.г - а)/2(7]/о-\/27г при общем среднем а = 3 и различных а . Параметр а - это среднеквадрати-ческое отклонение (квадратный корень из дисперсии). ФР нормального распределения выражается через функцию Лапласа

Ф{х)

(.3.3.10)

согласно

(3.3.11)

Рисунок наглядно иллюстрирует концентрацию значений случайной величины в окрестности среднего значения (точнее, математического ожидания) при уменьшении среднеквадратического отклонения. Площади под каждой кривой одинаковы, поскольку для любой плотности

J f[x)dx - 1 . Отличия нормального распределения от других, имею-

- ОС

щих те же среднее и дисперсию, можно охарактеризовать асимметрией S - рз/а и эксцессом е = Рл/ - 3. В этих формулах {pi] суть центральные моменты, вычисленные относительно среднего.

Эта технология ниже рассматривается для распределения Вейбулла.