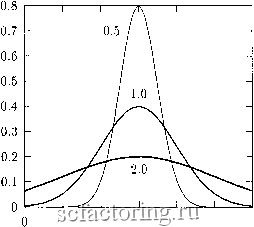1 2 3 4 5 6 Рис. 3.4. Нормальные плотности

3.3.4. Распределение Вейбулла

Основным показателем качества функционирования многих СМО является ДФР времени пребывания заявки в системе, получаемая в виде таблицы для заданных значений аргумента. Неинтегрируемость гамма-плотности вынуждает искать для вычисления ДФР по заданным моментам другую аппроксимацию. Удобно применение распределения Вейбулла

F{t) = e-. (3.3.12)

Его моменты

Л= (0r(0iy/= = W/=r(l + iA), j = l,2,..., (3.3.13)

а отношение

а = hlfl = 2кГ(2/к)/Т\1/к) = 2Т{2и)/(иТ\и)),

(3.3.14)

где и = 1/к. Воспользовавшись формулой удвоения аргумента гамма-функции, можно переписать (3.3.14) в виде

2 Г(ц)Г(ц+1/2) 2 Г(ц + 1/2)

откуда следует обеспечивающая быстро сходящийся итерационный процесс уточнения и формула

1 аГ(г/, 1 + 1) = 2Ы2 ГК Ч-1/2) - =

Начальное приближение

го = 1п2а/(21п2). (3.3.16)

При необходимости учета более двух моментов можно применить ту же базовую аппроксимацию с поправочным многочленом:

F(/) = e-Vvv..,.. (3.3.17)

Моменты этого распределения

. N

fj = i = OV. (3.3.18)

Теперь ясен алгоритм подбора параметров аппроксимации (3.3.17) по моментам {/j}, j = l,N :

1) Вычислить а - /2/fi

2) Определить щ согласно (3.3.16).

3) Решить уравнение (3.3.15) методом итераций.

4) Вычислить к = 1/и, W = {fi/T{u -f 1)) .

5) Сформировать систему (3.3.18) линейных алгебраических уравнений относительно {gi}.

6) Решить эту систему любым стандартным методом.

3.3.5. Дискретные распределения

Дискретные распределения обычно задаются набором вероятностей появления допустимых значений.

Распределение Пуассона описывает вероятности редких событий:

р,-е-\ х = 0,1,... (3.3.19)

Биномиальное распределение получается при повторении независимых испытаний, каждое из которых имеет только два возможных исхода. Без потери общности эти исходы можно классифицировать как успех и неудачу , наблюдаемые с вероятностями р \л 1 - р соответственно. Вероятность появления х успехов в п испытаниях равна

Рх - ,

p-(l-/>)- 0 = 0, п. (3.3.21)

Для биномиального распределения

М[Х]=1пр, D[X]np{l- р). (3.3.22)

Отрицательное биномиальное распределение

= . = 0,1,...

(3.3.23)

дает вероятности того, что потребуется ровно х -\- п испытаний для получения п успехов. Здесь

М[Х] = п(1-р)/р, D[X] = n{\-p)/p\ (3.3.24)

Геометрическое распределение является его частным случаем ( п = 1). Здесь

p, = p(l-p) ;г = 0,1,..., (3.3.25) а числовые характеристики

М[Х] = (1 -р) >, D[X] = {1-р)/р\ (3.3.26)

3.4. Преобразования распределений

Для некоторых вероятностных расчетов удобно пользоваться преобразованиями распределений. В случае непрерывных распределений

Здесь Л - интенсивность потока редких событий, at - время наблюдения. Для этого распределения

М[Х] = D[X] = М. (3.3.20)