

 |
 |
|
Факторинг Распределение и корреляция приращений Могут произойти три ситуации, проиллюстрированные Рис. 71, Рис. 72 и Рис. 73. Давайте обсудим их в контексте модели имитативного поведения, представленного в главе 4 и резюмированного эволюционным уравнением (6). Вспомним, что в данной модели агенты имеют склонность подражать друг другу согласно силе склонности К, количественно определяющей относительную силу подражания по сравнению с идиосинкразическим взглядом. Большая К ведет к сильной организации, где большинство агентов разделяют одинаковое мнение. Малая К соответствует группе, разделенной пополам между двумя мнениями, так чго пространственная организация агентов разрознена. Посредине, как мы показали в главе 4, существует критическая величина отделяющая эти два крайних режима, при которой система является критической, то есть шкала инвариантна. Группа перенормироюк делает даннью утверждения точными, что и показано на Рис. 71, Рис. 72 и Рис. 73. . - . .--i. : - с-, v. . .- ::  Рис. 72. Данный рисунок иллккприрует эффект перенормировки для КЖс изинговской модели (6), чго соответствует упорядоченному режиму, в котором одно мнение (белое) доминирует (два различных мнения обозначены черным и белым). Начиная слева с квадратной решетки с некоторой заданной конфигурацией мнений, на рисунках справа показаны два успешных применения фуппы перенормировки. Мы видим постепенное изменение структуры решетки со все большей организацией (один цвет, то есть мнение, доминирует все больше и больше). Все более короткие корреляционные интервады устранены с помощью процесса перенормировки, и система становится все более и более упорядоченной, соответствующей действующему увеличению силы подражания К. Система отводится от критичности с помощью перенормировки. Ренормфуппа, таким образом, квалифицирует данный режим как упорадоченный при изменении масштаба. 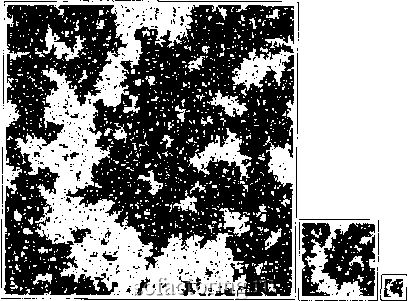 Рис. 73. Данный рисунок демонстрирует действие перенормировки для К=Кс изинговской модели (6), что соответствует критической точке. Два различных мнения обозначены черным и белым. Повторные применения ренормгруппы оставляют структуру решетки статистически инвариантной. Все более короткие корреляционные интервады устранены с помощью процесса перенормировки; однако система поддерживает то же равновесие ме)кду порядком и беспорядком и действующая сила имитации остается неизменной и фиксированной при фитическом значении Кс Система удерживается в фитичности при помощи перенормировки. Ренормфуппа, таким образом, квалифицирует данный р®ким как фитический, характеризующийся инвариантной симмефией шкады. Другими словами, система фупп и мнений является фрактадьной. Фрактальная функция Вейерштрасса: сингулярное, зависящее от времени решение группы перенормировки. Непосредственно в фитической точке инвариантность шкалы точно вьшолняется. Она нарушается либо на самом маленьком масштабе, если имеется минимальная масштабная единица, и/или в самом большом масштабе, соответствующем конечному размфу системьт Между этими офаничивающими масштабами система является фрактальной. Эго описание остается верным и не За исключением особого критического значения применение ренормгруппы отводит систему от критического значения. Можно использовать данный поток в пространстве систем, чтобы точно рассчитать критические показатели степени, характеризующие отклонение измеряемых величтш при приближении к критическим точкам. Критические показатели степени играют роль функции управления данным потоком; то есть они описьтают скорость отдаления от критической точки. только в критической точке непосредственно, однако, лишь до такого уровня масштаба, который называется корреляционной длгаюй, и который теперь шрает ту же роль, что и конечный размер системы в критической точке. Рис. 48 показал нам, что длина корреляции является размером самой большой группы, то есть расстоянием, на котором локальные подражания среди соседей распространяются прежде, чем шум сделает их в значительной степени беспорядочными в процессе передачи, возникающем от идиосинкразических сигналов каждого агента. Это значит, что математическое вьфажение (8), вьфажающее точную инвариантность шкалы более не является абсолютно верным и должно быть несколько видоизменено. Группа перенормировки дает нам ответ и показывает, что необходимо ввести новый член в правую часть вьфажения (8). Этот новый член передает эффект степеней свободы, забытый при процедуре грубой обработки при помощи фуппы перенормировки, при переходе от одного масштаба к большему. 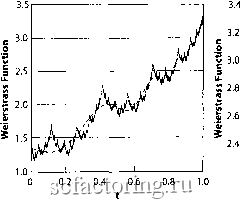 2.2 0.8
0.85 0.9 t 0.95 Рис. 74. Функция Вейерштрасса, определяемая как решение уравнения фуппы перенормировки, полученное из точного самоподобного критического выражения (8), путем добавления простой косинусо1зды, включающей в себя действие степеней свободы на малых масштабах на следующем, большем масштабе. Функция Вейерштрасса демонсфирует свойство самоподобия, что в1адно при сравнении увеличенной области на правом рисунке с левым рисунком. Существует бесконечно разветвленный набор сфуктур, концентрирующихся по мере приближения критического времени tc=l Самоподобие описывается фрактальной размерностью, равной 1,5. Сингулярность степенной зависимости при fcrt описывается показателем степени а=М2. Медленно осциллирующая пунктирная линия, охватывающая крупномасштабную сфуктуру функции Вейерштрасса, является простой степенной зависимостью 3,4ifWf с критическим показателем степени Уг, осложненным логопериодической осцилляцией cos(2nLn(t(rt)/Ln2), показывающей, что доминирующим дискретным масштабным коэффициентом является в данном примере А=2. Повторение остроконечных структур, таким образом, происходит в правильной геометрической логопериодической манере, с основной логопериодичностью, заданной в данном примере А=2. Математическое преобразование (называемое фансформантой Меллина (Mellin)) кроме этого показывает, что существует бесконечная иерархия гармоник этой основной логопериодичности для всех целых степеней А=2, несущая ответственность за слеп<а волнистую структуру на всех масштабах. 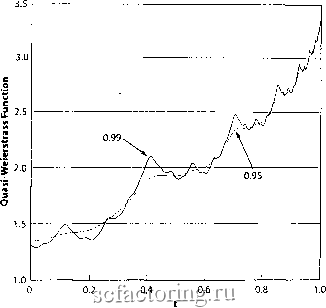 Рис. 75. То же, что и на Рис. 74, но с заменой косинусоидальной функции на экспоненциально ослабленную косинусоидальную функцию, чей коэффициент затухания равен 1 минус число, обозначенное на стрелках. Эта квази-функция Вейерштрасса более не является абсолютно фрактальной, поскольку она становится гладкой в малом масштабе. Обратите внимание, что логопериодичность сохраняется на больших масштабах, но разрушается на малых. 7(рмпле{Ъ1ефршпальнъш размерности и логопериодичность Сейчас мы в состоянии интуитивно понять описание дискретной масштабной инвариантности, представленное ранее в данной главе. Как мы отмечали прежде, дискретная масштабная инвариантность есть не что иное, как более слабый вид масштабной инвариантности, согласно которому система или измеряемая величтша подчиняются масштабной инвфиантности, как определено выше, только для специфических выборов коэффициентов увеличения или При выборе этого нового члена в виде простой косинусоидальной функции cos(x), соответствующей регулярным осцилляциям, решение уравнения группы перенормировки оказывается равным знаменитой функции, называемой функцией Вейерштрасса (Weierstrass) [44, 117]. Данная функция, показанная на Рис. 74. имеет замечательное свойство быть непрерывной, но нигде недифференцируемой. Интуитивно непрерывность означает, что в ней нет дьф . Недифференцируемость означает, что мы не можем определить локальный тангенс угла наклона; то есть кривая является негладкой на всех масштабах. В примере, показанном на Рис. 75., кривая Вейерштрасса является критической при 4=i. Помимо этого, она характеризуется самоподобной ифархией логопериодических сфуктур, концешрирующихся к критическому времени tc=l. разрешения L Эт коэффициенты формируют в целом бесконечное, но счетное множество значений h, h которое может быть записано как целый показатель степени у1 = А . А - это фундаментальный коэффициент масштабирования (scaling ratio). Очевидно, что две иерархические сети на Рис. 62 и Рис. 66 подчиняются дискретной масштабной инвариантности, но не (непрерывной) масштабной инвариантности. Действительно, по своей конструкции ромбовидная решетка точно восстанавливается только при паличтш дискретного ряда коэффициентов, определяющих последовательные увеличения, которые заменяют каяодую связь четырьмя новыми связями, каадую из четырех связей четьфьмя новыми связями и так далее. В том же роде, дихотомическое дерево является инвариантным только при дискретном множестве увеличений, когда каждая ветвь удваивается в дискретной иерархии. Действительно, все обычные фрактальные консфукции наделены симмефией дисфетной масштабной инвариантности. Знаменитыми примерами являются канторово (Cantor) множество, феугольник Серпинского (81еф1п8ку), снежинка Коха (Koch), а также многие другие примеры[284]. Мы увидели, что отличительным признаком масштабной инвариантности является существование степенной зависимости, офажающей факт отсутствия предпочтительньк шкал. Показатели степени в этих степенных зависимостях определяют фрактальные размфности. Признаком дисфетной масштабной инвариантности становится существование логопфиодических осцилляции, усложняющих степенные зависимости. Как мы увидим, эти логопериодические Сфуктуры могут быть представлены математически, при помотци того факта, что показатель степени а или, что одно и то же, размерность d, является не только нецелочисленным, но и становится комплексным числом. Мы увидели, что непрерывная масштабная инвариантность дает толчок к появлению нецелочисленных (действительных) фрактальных размфпостей. Тепфь мы утвфждаем, что дисфсгаая масштабная инвариантность характеризуется комплексными фрактальными размерностями. Прежде, чем мы подтвердим данное утвфждение примфами, давайте немного порассуждаем по поводу чудесного примера невероятной достаточности математики для описания природных явлений: поиск более эстетически приятной всеобщности и логичной последовательности в математике, в конечном итоге, охватьгоает всеобщность глубокой концепции. Уигнф (E.P.Wigner), лауреат Нобелевской премии в области физики за работу по симмсфиям в ядфпой физике и квантовой механике, сформулировал ее следующим образом [246]: Невфоятная польза математики для естественных паук является чем-то, фаничашцм с волшебством... Замечательное свойство язька математики подходить для формулировки физических законов является чудесным даром, которого мы не только не понимаем, но и не заслуживаем . Комплексные числа составляют самое общее множество чисел, подчиняющихся стандартным правилам сложения/вычитания и умножения/деления. Они содфжат, в частности, целые числа О, 1, 2, 3,... и действительные числа, такие как любое число с целой и десятично-дробной частью, как 876,34878278.... Дроби двух целых чисел, такие как 13/8 являются специальными действительными числами, назьгоаемыми рациональными,
Рис. 76. Кол/1плексная плоскость: Горизонтальная линия представляет действительные числа, которые включают в себя, в частности, целые числа -3, -2, -1,0,1,2,3... Вертикальная линия представляет собой абсолютно к/1нимые числа, произведение / на произвольные действительные числа. Оставшаяся плоскость является совокупностью недействительных коллплексных чисел. Терлчины кол/тлексные и л/1нил/1ые подчеркивают мысль, что данные числа находятся за пределами действительных чисел и наблюдаются как проекции или тени на действительной оси. Любое комплексное число эквивалентно пфе действительных чисел. Первый член пфы пазьшается действительной частью комплексного числа. Второй член пары называется мнимой частью. Если второй член равен О, то комплексное число редуцируется до чисто действительного числа. В то время, как действительное число может рассмафиваться как точка на прямой, комплексное число есть не что иное, как представление точки па плоскости, как показано на Рис. 76, такое, что пара чисел, составляющих комплексное число, соответствует двум координатам или проекциям, соответственно, на горизонтальной и вертикальной осях. Мнимая часть комплексного числа пропорциональны их основному представителю , обозначаемому символом i , который таков, что его квадрат г=ш равен -1. Неспециалисту данное свойстю может показаться неестественным, похожим па волшебный фокус, по математикам нравится определять объекты, обладающие самыми общими свойствами, которые, тем не менее, согласуются с предшествовавшими правилами, в данном случае - со стандартными правилами сложения/вычитания и умножения/деления. Свойство f = -1 оказьгоается естественным, если толкуется как действие па плоскости, а не только вдоль оси поскольку они Хфактеризуются либо конечной десятичной дробной частью (13/8=1,625), либо бесконечной, по периодической десятичной дробной частью, напримф, 13/11=1,181818181818..., где элемент 18 повторяется до бесконечности! Большая часть действительных чисел, позволяющая инженфам производить расчеты длины, веса, силы, сопротивления и так далее, в принципе, характеризуются бесконечной неповторяющейся дробной десятичной частью! Множество всех действительных чисел может быть представлено в виде пепрерьгепой линии, каждая точка па которой точно соспБетствуег единственному действительному числу. Таким образом, действительные числа являются отметками, точно указьгоающими положение вдоль линий, как показано на Рис 76 и Рис. 77.
|
||||||||||||||||||||||||||||||||||||