Береговые линии являются хорошим примером, особенно если провести параллель между ними и временными рядами. Мандельброт (1982) выдвинул постулат о том, что мы никогда не сможем измерить действительную длину береговой линии, поскольку измеряемая длина зависит от длины используемой для измерения линейки.

Предположим, например, что мы хотим измерить длину побережья штата Мэн. Мы начнем с самой северной точки и будем мерить, накладывая на поверхность земли линейку шестифутовой длины. Мы будем складывать шестифутовые приращения, двигаясь вниз по берегу, и придем к какому-то числу. Затем мы повторим эту процедуру, используя трехфутовую линейку. На этот раз мы сможем уловить больше деталей, так как линейка наша короче. Поскольку мы сможем учесть большее ко:гичество бухточек и фиордов, мы в итоге получим большую длину побережья. Если мы укоротим линейку еще на один фут, то получим еще больше деталей и еще большую длину. Чем короче будет становиться линейка, тем длиннее береговая линия. Получается, что длина береговой линии зависит от размеров линейки!

Ввиду того что это справедливо для всех береговых линий, длина как мера не годится для сравнения береговых линий. Вместо нее Мандельброт предложил использовать фрактальную размерность. Береговые линии представляют собой зазубренные кривые, поэтому их фрактальная размерность больше едиргицы (т. е. их евклидовой размерности); то, насколько она больше единицы, зависит от степени зазубренности. Чем она больше, тем ближе размерность береговой линии к ДВУМ - раямррности птоскости

Фрактальная размерность рассчитывается посредством измерения этого свойства зазубренности. Мы подсчитываем количество окружностей определенного диаметра, которое необходимо для покрытия береговой линии. Мы увеличиваем их диаметр и снова считаем их количество. Продолжая эту процедуру, мы найдем, что количество окружностей и их радиус связывает показательная зависимость:

АГ*(2*г) = 1, (6.1)

1е Л/ - количество окружностей, г -радиус окружности, ~ фрактальная размерность.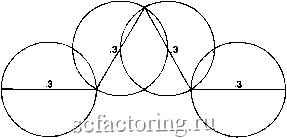

Рис. 6.1. Вычисление фрактальной размерности.

Уравнение (6.1) может быть приведено к отношению логарифмов:

log TV

log(l/2*r)

(6.2)

Можно использовать некоторую часть снежинки Кох в качестве простейшей береговой линии; средняя треть этой линии несет на себе равносторонний треугольник. Если длине этой ломаной цепочки равна единице, то тогда нам нужно четыре окружности диаметром 0.3, чтобы покрыть эту кривук (см. рис. 6.1). Фрактальная размерность кривой Кох будет равна:

log(4) log(l/0.3)

= 1.26.

Реальные берегпые линии утрорньт аналогичныл обпа-зом. Береговая линия Норвегии, например, имеет фрактальную размерность, равную 1.52, в то время как берег Британии-1.30. Это означает, что береговая линия Норвегии более изрезана, чем в Британии, и поэтому ее размерност! ближе к 2.00. Подобным же образом мы могли бы сравни вать разные акции - посредством указания их фрактальиьп размерностей. Обычно мы сравниваем риски различных цен ных бумаг посредством оценки их волатильности. Эта концеп ция была впервые широко представлена в работе Марковицг (Markovitz, 1952); она предполагает, что чем выше волатиль ность акции, тем выше ее уровень риска. Волатильность, ил1 риск, утверждался в качестве статистической меры, будуч! представленным как стандартное отклонение прибылей - ил1

их квадратов, т. е. дисперсий. Волатильность предлагают измерять дисперсией прибылей, не так ли?

Стандартное отклонение измеряет вероятность того, что наблюдение будет располагаться на определенном расстоянии от среднего. Чем больпхе это расстояние, тем больше рассеяние. Большое рассеяние означало бы, что существует высокая вероятность больших колебаний прибыли. Такая ценная бумага обладает высоким уровнем риска. Однако часто упускают из виду, что стандартное отклонение как мера рассеяния подходит только для случайных систем. Если наблюдения коррелированны (или имеют серийную корреляцию), то тогда польза стандартного отклонения как меры рассеяния в значительной степени снижается. Поскольку многочисленными исследованиями установлено (см. гл. 3), что распределение прибылей акции не следует нормальному распределению, стандартное отклонение как мера сравнения уровней риска ставится под вопрос.

Рассмотрим для примера два ряда возможных прибылей, обозначенных 5i и 52 в таблице 6.1. Ряд 52 не нормально распределен и имеет выраженный тренд. Ряд 5i не показывает тренда и имеет накопленную прибыль 1.93%, в то время как 52 имеет 22.83%. Однако 5i имеет стандартное отклонение 1.70, в то время как 52 имеет фактически то же самое стандартное отклонение -1.71. В этом гипотетическом примере две акции с фактическими одинаковыми волатильностя-ми имеют совершенно различные характеристики прибылей. Пуристы скажут, что оба ряда не нормально распределены, и это делает их сравнение невозможным. Это совершенно вер-

Таблица 6.1. Стандартное отклонение в сравнении с фрактальной размерностью.

людение

Накопленная прибыль

тандартное отклонение ктальная размерность

+2 -1 -2 +2 -1 +2

+1.93 1.70 1.41

+6 +22.83 1.71 1.13