При неизменности начального капитала и повторяющейся игре с постоянной ставкой вероятность разорения будет минимальной при выборе такой ставки, которая была бы совместимой с суммой желаемого выигрыша.

Пример 2. Рассмотрим ту же невыгодную игровую ситуацию, при которой q = 0,55, р = 0,45. И пусть z = 90, а w = 100 условных единиц .

Если при каждом испытании ставка будет равной одной условной единице , то вероятность разорения, действительно, составит почти предельную величину:

Q(z = 0) = 0,866.

Но если увеличить ставку до максимально возможного значения (при заданных условиях оно равно w - z = 100 - 90 = 10), то столь неблагоприятный прогноз меняется кардинально. И хотя математическое ожидание выигрыша остается тем же, вероятность разорения составит всего лишь 0,210, а выигрыша - возрастет до 0,790.

Как видим, несмотря на неблагоприятное соотношения р и q, у обреченного игрока есть значительные шансы выйти победителем в какой-то из попыток.

Разумеется, эту победу можно сохранить лишь тогда, когда игрок имеет право тут же раскланяться и удалиться подальше от места игры.

2. По существу, близкие к этим результаты можно получить и для испытаний с идеальной монетой (q =р).

Правда, вышеприведенная формула оценки вероятности разорения здесь не годится. Выведена более простая:

Q(-z) = 1 - (z/w),

где (w - z) > О - чистый выигрыш.

Тогда вероятность такого исхода:

P(z) = 1 - Q(-z) = z/w.

Если исследовать зависимость функции Q(z/w) от соотношения переменных Z и W, то обнаруживается следующее (см. рисунок 13).

При некотором заданном постоянном значении z (z = const) вероятность разорения уменьшается по мере изменения величины w в сторону сближения с Z. И вероятность разорения достигает минимальных значений, когда величины W и Z становятся сравнимыми (z ~ w).

Это правило можно сформулировать таким образом:

вероятность разорения в игре с постоянной ставкой становится минимальной при малом в сравнении с исходным капиталом z

выифыше как цели игры и максимально приближенной к чистому выигрышу (w - z) ставке.

При р = q вероятность разорения Q становится минимальной, а выигрыша Р - максимальной при двух условиях: 1) минимальная цель выигрыша; 2) максимальная ставка.

Y = Q(z/w)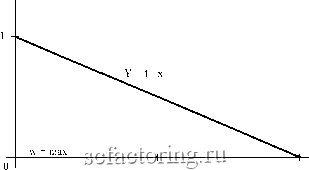

Z W Z = 0,5w z - w

Рисунок 13. функция Y = 1 - X (гдех = z/w, ног<ш)

Пример 3. (это условия примера 2, но только для значения q = р). При ставке, равной 0,lz, получим, что:

W = Z + 0,lz.

И тогда вероятность разорения

Q(-z) = 1 - (z/w) = 1 - z / (z + 0,lz) = = 1 -10 / 11 = 1 /11 = 0,09.

A вероятность выигрыша

P(w) = 0,1/1,1 = 0,91.

Приведем в этой связи некоторые расчеты для соотношений, с которыми реально имеет дело трейдер-индивидуал.

При этом обратим внимание на два суш;ественных момента, касаюш;ихся условий игры:

1) ставка является аналогом стоп-ордера по прибыли (stop-profit) в каждом отдельном испытании (срабатывании сигнала );

2) исходный капитал z выполняет одновременно две функции: и стоп-ордера по убытку (stop-loss), и ордера стоп-операция .

Пусть игрок имеет начальный капитал в $3000. Ставка (stop-profit) при каждой игре составляет $300. Это происходит при стоп-ордере в 30 базисных пунктов при операциях с британским фунтом стерлингов (GBP), скажем, против доллара США.

Тогда имеем условия: z = 3000 и w = 3300.

Но поскольку в качестве условной единицы служит величина $300, то в масштабе исчисления, использованного выше, это означает, что z = 10, а w=z + 0,lz = ll.H мы приходим к условиям и решениям примера 3, где: Q(-z) = 0,09 и P(w) = 0,91.

Как видим, при неблагоприятном соотношении р < q можно, управляя значениями w, z и размером ставки, добиться впечатляюще хороших пропорций Q(z) и P(w).

Математическое ожидание результата. Под математическим ожиданием выигрыша здесь понимается средний результат испытаний, который ожидается при повторении одной и той же игры.

В этой связи возникает вопрос о том, каково математическое ожидание результата, т.е. средний выигрыш в ходе продолжительного повторения игры, при условиях:

неблагоприятного соотношения р < q;

благоприятного соотношения Q(-z) < P(w).

Как следует из условий, конечный результат игры ( победа w или поражение Z = 0) - это случайная переменная, которая принимает одно из двух значений:

(W-Z);

(-Z).

Тогда математическое ожидание выигрыша (Е) для любого, в том числе и равного, соотношения q и р*:

Е = P(w) X (w - z) - Q(z = 0) X (-Z) = w X P(w) - z.

A при q = p:

E = wx{l-Q(z = 0)}-z.

Если в эти формулы подставить значения Q(z = 0), то получим: Е(для q > р) < О